دسته: جذبی

اواپراتور

• اواپراتور یا تبخیر کننده، بخش خنک کن چیلر جذبی محسوب می شود.
• اواپراتور مبدلی است که در آن آب تغذیه فن کوئل ها و هواسازها، گرمای خود را به مبرد می دهد و خود خنک شده و موجب تبخیر مبرد می شود.
• اواپراتور در واقع یک مبدل پیوسته و لوله است که آب سرد رفت و برگشت در لوله های آن جریان می یابد و مبرد در فضای پیوسته تبخیر می شود.
• به طور معمول لوله های این مبدل از جنس مس و پوسته، فولادی است.
• در محفظه اواپراتور و در طول آن کلکتوری مجهز به افشانک هایی نصب می شود تا مبرد(آب) را در فضای آن و بر روی کوئل پاشیده تا از این طریق مقدار تبخیر افزایش یابد.
• تشتک اواپراتور و افشانک ها از فولاد کربنی ساخته می شوند.
• یک پمپ به طور مرتب مبرد را از تشتک اواپراتور(بخش زیرین پوسته) مکش نموده و از طریق کلکتور و افشانک ها در فضای اواپراتور می پاشد.
• به منظور ممانعت از اتلاف حرارت، سطوح خارجی پوسته ی اواپراتور عایق می شود.
• در چیلرهای شعله مستقیم ، اواپراتور ها در فصل زمستان نقش مبدل گرمایشی را به عهده گرفته و به کمک بخار گرم محلول، آب در گردش را گرم می کنند. تحت این شرایط بر اساس مقررات ARI 560 حد اکثر دمای آب خروجی 60 درجه ی سانتی گراد(140 درجه فارنهایت) تعیین شده است.
• فشار داخل اواپراتور 6 میلی متر جیوه(0.8) کیلو پاسکال است و تحت این فشار مبرد(آب) در دمای 3.9 درجه سانتی گراد(39 درجه فارنهایت) تبخیر می شود.
• شرایط استاندارد برای دمای آب خروجی از اواپراتور مطابق ARI 560 برای انواع چیلرهای یک اثره، دو اثره و شعله مستقیم 6.7 درجه ی سانتی گراد(44 درجه فارنهایت) است.
• شرایط استاندارد برای دبی آب سرد جاری در کوئل اواپراتور که تجهیزات تبادل حرارت ساختمان را تغذیه می کند بر اساس ARI 560 برای انواع چیلرهای یک اثره، دو اثره و شعله مستقیم، 2.4 گالن بر دقیقه به ازای هر تن تبرید(0.043 لیتر بر ثانیه به ازای هر کیلو وات) است.
• ضریب رسوب گذاری لو له های اواپراتور که آب تغذیه ی تجهیزات تبادل حرارت در آن جریان می یابد مطابق ARI 560 برای انواع چیلرها، 0.000018 m² C/W (0.00001 ft² F/Btuh) است.

ابزوربر 

• ابزوربر حاوی ماده ی جاذب(محلول لیتیم بروماید) است.
• محفظه جاذب نیز همچون اواپراتور یک مبدل پوسته و لوله است که در لوله های آن، آب برج خنک کن جریان می یابد و پوسته حاوی لیتیم بروماید است.
• محلول رقیق در ابزوربر تشکیل می شود.
• عمل تبخیر در اواپراتور توام با اخذ گرما از کوئل حاوی آب ساختمان است. بنابراین دمای ابزوربر به هنگام جذب بخار مبرد افزایش می یابد. آب خنک برج، بخشی از گرمای آزاد شده در ابزوربر را گرفته و آن را از سیستم دفع می کند تا این محفظه برای جذب بهتر تا حد مشخصی خنک بماند.
• کاهش بیش از اندازه ی دما در ابزوربر تبعات ناخوشایندی همچون متبلور شدن محلول را به همراه خواهد داشت.
• ابزوربر نیز همچون اواپراتور دارای کلکتور و افشانک هایی است که محلول از داخل آن به روی کوئل پاشیده شده و به این ترتیب با سرد شدن هر چه بیشتر آن، بازده جذب بالاتر رفته و بخار آب بیشتری از محفظه ی اواپراتور جذب لیتیم بروماید می شود.
• برخی از چیلرها دارای پمپ مخصوصی به عنوان پمپ ابزوربر هستند که وظیفه آن مکش محلول از تشتک(بخش زیرین پوسته ابزوربر) و دهش آن به داخل فضای ابزوربر از طریق کلکتور و افشانک ها است.
• در برخی مدل های دیگر نیز این عمل بدون پمپ و به صورت ثقلی انجام می شود، زیرا ژنراتور در ارتفاعی بالاتر از ابزوربر قرار می گیرد. بنابراین محلول خروجی از ژنراتور از طریق کلکتور و افشانک ها بدون نیاز به پمپ وارد ابزوربر می شود. چیلرهای با ظرفیت بالا نیازمند استفاده از پمپ سوم نیز هستند.
• در قسمت زیرین ابزوربر، پمپ دیگری با نام پمپ محلول وجود دارد که محلول رقیق را از مبدل حرارتی گذرانده و آن را به ژنراتور می ریزد.
• ابزوربر و اواپراتور در پوسته ای مشترک جای می گیرند و از داخل به هم مرتبط هستند. به این ترتیب بخار حاصل از تبخیر مبرد به طور مستقیم جذب لیتیم بروماید موجود در ابزوربر می شود. در برخی مدل ها اواپراتور بالای ابزوربر قرار می گیرد و تحت این شرایط احتمال نفوذ لیتیم بروماید به اواپراتور کاهش می یابد. در بعضی مدل های دیگر اواپراتور و ابزوربر به صورت افقی و در کنار یکدیگر قرار می گیرند. در هر حال در هر دو مدل برای جداسازی این دو محفظه از صفحات قطره گیر(Eliminator) استفاده می شود تا ضمن امکان برقراری ارتباط مستقیم از نفوذ لیتیم بروماید به محفظه اواپراتور جلوگیری شود.
• شرایط استاندارد برای دمای آب برج خنک کننده ورودی به ابزوربر بر اساس مقررات ARI 560 برای انواع چیلرهای یک اثره، دو اثره و شعله مستقیم، در بار کامل 29.4 درجه ی سانتی گراد(85 درجه ی فارنهایت) تعریف شده است و برای بارهای جزئی 75 درصد  25.3 درجه ی سانتی گراد(77.5 درجه ی فارنهایت) و برای بارهای جزئی 50 و 25 درصد، 21.1 درجه ی سانتی گراد(70 درجه ی فارنهایت) مشخص شده است.
• شرایط استاندارد برای دبی آب برج خنک کننده ابزوربر و کندانسور بر اساس استاندارد ARI 560 برای چیلرهای یک اثره 3.6 گالن در دقیقه به ازای هر تن تبرید(0.065 لیتر بر ثانیه به ازای هر کیلووات) بر اساس (9°C) 17°F اختلاف دمای آب برج خنک کننده و برای چیلرهای دو اثره و شعله مستقیم 4 گالن بر دقیقه به ازای هر تن تبرید(0.072 لیتر بر ثانیه به ازای هر کیلووات) بر اساس(7°C) 12°F اختلاف دمای آب برج خنک کننده است.
• ضریب رسوب گذاری(Fouling Factor) لوله های ابزوربر که مجرای گردش آب برج خنک کننده محسوب می شوند مطابق مقررات ARI 560 برای انواع چیلرهای یک اثره، دو اثره و شعله مستقیم 0.000044 متر مربع کلوین بر وات(0.00025 ft2 f/btu h) است.

ژنراتور  

• عملیات تغلیظ محلول لیتیم بروماید در ژنراتور انجام می شود.
• چیلرهای یک اثره دارای یک ژنراتور هستند که ممکن است با آب گرم، آب داغ و یا بخار گرم شود.
• برخی ژنراتورها نیز مانند اواپراتور و ابزوربر دارای افشانک هایی هستند که محلول رقیق از طریق آن ها در فضای پوسته پاشیده می شود تا در تماس با کوئل گرم حاوی بخار یا آب گرم، لیتیم بروماید محلول از بخار آب(مبرد) جدا شود. اما در بسیاری از مدل ها از هیچگونه تشتک توزیع یا افشانه ای برای ریزش محلول رقیق به درون ژنراتور استفاده نمی شود.
• چیلرهای دو اثره دارای دو ژنراتور دمای زیاد و کم هستند که لیتیم بروماید در آنها به صورت مرحله ای تلغیظ می شود. ژنراتور دمای زیاد به طور مستقیم از طریق منبع حرارتی جداگانه(آب گرم یا بخار) تغذیه می شود و گرمای ژنراتور دمای کم، از طریق بخار مبرد حاصل از عملیات تلغیظ در ژنراتور دمای زیاد، تامین می شود.
• چیلرهای شعله مستقیم نیز هم چون چیلرهای دو اثره دارای دو ژنراتور دمای کم و زیاد هستند. در این گونه چیلرها ژنراتور دمای زیاد در واقع نوعی دیگ فولادی متصل به چیلر است و به کمک شعله مستقیم مشعل عملیات تلغیظ اصلی را انجام می دهد. ژنراتور دمای کم نیز هم چون چیلرهای دو اثره از طریق بخار مبرد جدا شده از محلول رقیق تغذیه می شود.
• ژنراتور چیلرهای یک اثره و همچنین هر دو ژنراتور چیلرهای دو اثره و ژنراتور دمای کم چیلرهای شعله مستقیم نوعی مبدل پوسته و لوله هستند که از میان لوله ها، سیال های گرمی چون آب گرم، آب داغ و بخار عبور می کنند و محلول رقیق در فضای پوسته غلیظ می شود. ژنراتور دمای زیاد چیلرهای شعله مستقیم، ساختاری مشابه دیگ های فولادی لوله آتش دارند که آتش و هوای گرم ناشی از احتراق از داخل کوره و لوله های فولادی حرکت نموده و محلول، رقیق در فضای پوسته دیگ غلیظ می شود. این گونه ژنراتورها بنا به ظرفیت چیلر ممکن است یک پاس(یک گذر) یا دو پاس(دو گذر) باشند. در چیلرهای شعله مستقیم ژنراتورهای دمای زیاد نقش مولد گرمایشی در زمستان را هم بازی می کنند.
• مطابق ARI 560، فشار بخار ورودی به ژنراتور چیلرهای یک اثره حداکثر15psip)103 Kp) با 2psi (14Kpa) افزایش و کاهش و بر اساس همین مقررات، حداکثر فشار ورودی بخار به چیلرهای دو اثره 125psig (861 Kpa ) با 15psi (103 Kpa ) کاهش و افزایش، تعیین شده است.
• دمای آب گرم یا آب داغ ورودی به ژنراتورهای چیلرهای یک اثره مطابق ARI560 بین 82 تا 204 درجه سانتی گراد(180 تا 400 درجه فارنهایت) تعیین شده است.
• ضریب رسوب گذاری مطابق ARI560 برای ژنراتورهای بخار باید صفر باشد و برای ژنراتورهای آب گرم یا داغ برابر0.000018m2C/W(0.00001 Ft2 f/Btuh ) تعیین شده است.

کندانسور   

• در محفظه ی تقطیر کننده یا کندانسور، بخار مبرد در تماس غیر مستقیم با آب ارسالی از سوی برج خنک کننده تبدیل به مایع می شود.
• در چیلرهای دو اثره و شعله مستقیم که دارای دو ژنراتور دمای کم و زیاد هستند، ژنراتور دمای کم در واقع خود نقش یک کندانسور را نیز بازی میکند، زیرا در این محفظه گرمای بخار مبرد صرف تلغیظ بخشی از محلول شده و خود تقطیر می شود.
• کندانسور هم مانند سه محفظه ای اصلی دیگر نوعی مبدل پوسته و لوله است که آب برج خنک کننده از میان لوله ها عبور نموده و عملیات تقطیر بخار آب در محفظه ی پوسته انجام می شود.
• شرایط استاندارد برای دمای آب برج خنک کننده ورودی به کندانسور بر اساس استاندارد ARI 560 برای انواع چیلر های یک اثره، دو اثره و شعله مستقیم، در بار کامل 29.4 درجه سانتی گراد(85 درجه فارنهایت) است و برای بارهای جزئی 75 درصد 25.3 درجه ی سانتی گراد(77.5 درجه ی فارنهایت) و برای بارهای جزئی 50 و 25 درصد ، 21.1 درجه ی سانتی گراد(70 درجه ی فارنهایت) است.
• شرایط استاندارد برای دبی آب برج خنک کننده کندانسور و ابزوربر بر اساس مقررات ARI 560 برای چیلر های یک اثره ، 3.6 گالن در دقیقه با ازای هر تن تبرید(0.065 لیتر در ثانیه به ازای هر کیلو وات) و برای چیلر های دو اثره و شعله مستقیم 4 گالن در دقیقه به ازای هر تن تبرید( 0.072 لیتر در ثانیه به ازای هر کیلو وات ) است.
• شریب رسوب گذاری(Fouling Factor) لوله های کندانسور که مجرای گردش آب برج خنک کننده محسوب می شوند مطابق ARI 560 برای انواع چیلرهای یک اثره، دو اثره و شعله مستقیم 0.000044 m2 K/W (متر مربع کلوین بر وات) ( 0.00025 ft2 f/btuh ) است.
• به طور معمول کندانسور بالاترین محفظه ی چیلرهای جذبی را تشکیل می دهد، از این رو مایع حاصل از عملیات تقطیر بدون نیاز به پمپ و به صورت ثقلی وارد اواپراتور می شود.
• محفظه ی کندانسور و ژنراتور در یک پوسته مشترک قرار می گیرند و از داخل به هم مرتبط هستند، بنابراین بخار آب ایجاد شده در ژنراتور به راحتی و به طور مستقیم وارد فضای کندانسور می شود.

مبدل حرارتی

• مبدل حرارتی امکان تبادل حرارت بین محلول رقیق خروجی از ابزوربر و محلول غلیظ خروجی از ژنراتور را فراهم می آورد. این مبدل نیز از نوع پوسته و لوله است که به طور معمول، محلول رقیق سردتر از میان لوله و محلول غلیظ گرم تر ازمیان پوسته عبور می کند.
• تبادل حرارت بین دو محلول رقیق و غلیظ موجب افزایش بازده ی سیستم می شود. زیرا پیش گرم نمودن محلول رقیق ورودی به ژنراتور موجب کاهش بار گرمایی در این محفظه شده و از سوی دیگر پیش سرد شدن محلول غلیظ قبل از ورود به ابزوربر باعث کاهش بار برج خنک کننده می شود.
• در چیلرهای دو اثره و شعله مستقیم متناسب با دو ژنراتور دمای زیاد و کم، دو مبدل حرارتی دمای زیاد و کم کاربرد دارد و در برخی مدل ها از مبدل حرارتی سومی نیز استفاده می شود. در این مبدل سوم، چگالیده حاصل از تقطیر بخار پس از خروج از ژنراتور در تماس غیر مستقیم با محلول ورودی به ژنراتور دمای بالا قرار می گیرد تا ضمن پیش گرم کردن آن، بخار احتمالی موجود در چگالیده قبل از ورود به تله بخار تقطیر شده و یا چگالیده با واگذاری گرمای محسوس خود به محلول، خنک تر می شود. این مبدل موجب افزایش کارایی چیلر می شود.

پمپ ها   

• پمپ های مبرد و محلول تنها قطعات مکانیکی مصرف کننده ی برق در چیلرهای جذبی محسوب می شوند.
• پمپ مبرد، آب را از تشتک اواپراتور مکیده و آن را از طریق افشانک ها یا نازل های تعبیه شده در فضای اواپراتور به روی کوئل حاوی آب سرد شونده می ریزد.
• پمپ محلول نقش انتقال محلول رقیق از ابزوربر به ژنراتور را به عهده دارد.
• در برخی چیلرهای جذبی از پمپ سومی، تحت عنوان پمپ ابزوربر نیز استفاده می شود. این پمپ محلول رقیق را از تشتک ابزوربر مکیده و آن را از طریق افشانک های تعبیه شده در فضای ابزوربر به روی کوئل آب برج خنک کننده می ریزد.
• پمپ های چیلرهای جذبی از نوع کاملا بسته(Hermetic) هستند.
• الکتروموتور و پمپ در یک پوسته کاملا درزبندی شده قرار دارند و انتقال حرکت از الکتروموتور به پمپ با محور مستقیم است.
• پمپ های چیلرهای جذبی از نوع گریز از مرکز است.
• مکش و دهش پمپ به لوله ها جوش داده می شود.
• به طور معمول در مسیر مکش و دهش پمپ هیچ گونه شیری نصب نمی شود، اما برخی از تولید کنندگان در مسیر مکش و دهش پمپ از شیرهای ربع گرد پروانه ای استفاده می کنند.
• یاتاقان های این نوع پمپ از نوع گرافیتی مخروطی بوده ونیازمند روغن کاری و خنک کاری خارجی نیستند و عملیات روان کاری و خنک کاری آن ها به وسیله مبرد یا محلول صورت می گیرد.
• این گونه پمپ ها نیازمند سرویس و نگهداری نیستند، اما بهتر است به ازای هر 50 یا 60 هزار ساعت مورد بازبینی قرار گیرند.
• توان الکتروموتورهای پمپ محلول و مبرد در ظرفیت های 100 تا 700 تن تبرید بین 3 تا 5 اسب(در حدود 2.2 تا 4 کیلو وات) است.
• به طور معمول ولتاژ الکترو موتورها 400 ولت سه فازه است.

پمپ خلا و سیستم جمع آوری گازهای غیر قابل تقطیر

• به منظور تخلیه هوا و گازهای غیر قابل تقطیر از پمپ خلا استفاده می شود.
• اگر چه پمپ خلا جزیی از ساختار اصلی چیلرهای جذبی محسوب نمی شود، اما بیشتر سازندگان ترجیح می دهند یک دستگاه از این گونه پمپ ها بر روی محصول خود نصب کنند. زیرا توصیه می شود که هر هفته حداقل یک بار، سیستم از هوا یا گازهای غیر قابل تقطیری که در اثر فعل و انفعالات شیمیایی یه وجود می آید، تخلیه شود.
• گازهای تولید شده که می باید به کمک سیستم تخلیه و پمپ خلا، هرازگاهی از چیلر خارج شوند، عبارتند از: ترکیبات مختلف نیتروژن مانند دی اکسید نیتروژن و تترا اکسید نیتروژن، مقداری آمونیاک و هیدروژن. در این میان هیدروژن سهم قابل توجهی را به خود اختصاص می دهد.
• تصاویر(3-29)،(3-30)،(3-31) نوعی سیستم جمع آوری گازهای غیر قابل تقطیر مجهز به پمپ خلا که بر روی برخی چیلرها نصب می شوند را نمایش می دهد. این سیستم دارای مخزنی است که گازها در آن جمع آوری می شود.
• در این مخزن، کوئلی جاسازی شده که در آن آب برج خنک کننده مدار کندانسور جاری می شود و از سوی دیگر لوله ای متصل به سمت دهش پمپ محلول، به طور مستمر مقداری از محلول خروجی از ابزوربر را به داخل این مخزن می پاشد. محلول ورودی به مخزن پس از تماس با کوئل کوچک آب برج خنک کننده و جدا سازی برخی گازهای غیرقابل تقطیر در بخش تحتانی مخزن جمع شده و از طریق خط مکش خارج می شود. نمونه ای از گازهای تولید شده در پوسته ابزوربر هم از طریق لوله ای وارد این مخزن می شود.

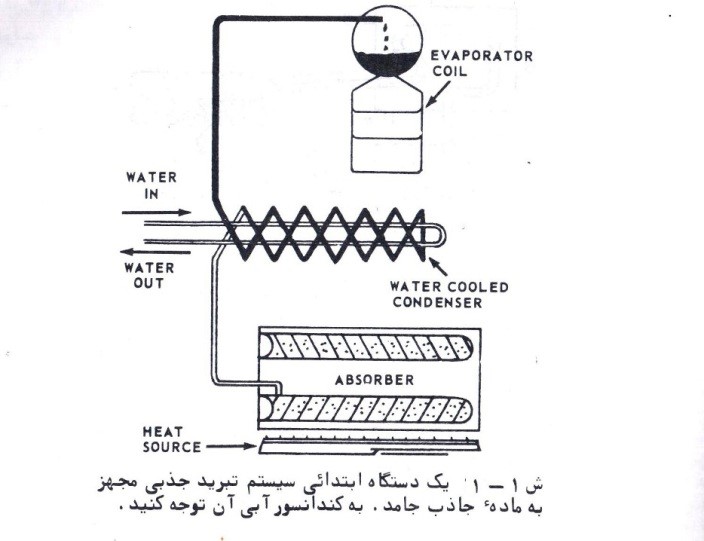
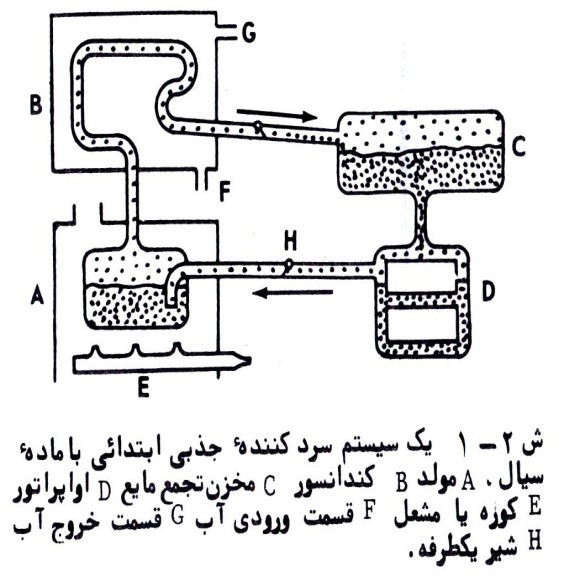
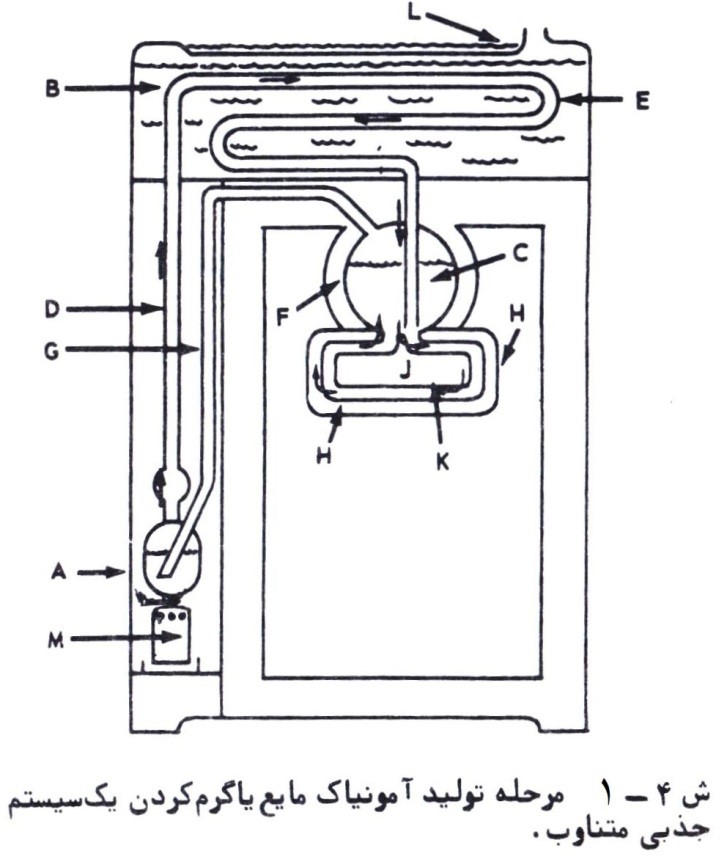
تحلیل ترمودینامیکی چرخه سرمایش

تبدیل انرژی به ویژه انرژی حراراتی و نسبت آن با حالت مواد، شاکله ی اصلی مباحث ترمودینامیکی است. از این رو موضوعات مرتبط با سرمایش و یا به عبارت دیگر کاهش گرما، بر پایه ی قواعد ترمودینامیک تحلیل می شوند.

یک سیستم ترمودینامیکی شامل فضا و کمیت مشخصی از مواد در حجمی مشخص است که به وسیله سطوحی از فضای خارج از این سیستم ، محیط اطراف خوانده می شود. مرزهای اطراف ممکن است ثابت یا غیر ثابت، واقعی یا فرضی باشند. این سیستم را می توان حجم کنترل نامید.

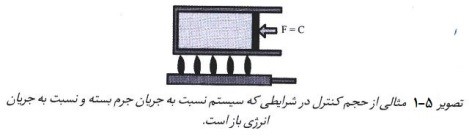
منظور از سیستم بسته، سیستمی نیست که نسبت به محیط اطراف کاملا ایزوله بوده و جریان انرژی و کار از مرزهای آن عبور نکند، بلکه این سیستم می تواند تحت تاثیر عوامل خارجی انرژی باشد، اما با محیط اطراف تبادل جرم نداشته باشد. منظور از بسته بودن سیستم مربوط به ساز و کار و چرخه ی عملکردی است. هر سیستم بسته ای می تواند در سیستم بسته دیگری جای گیرد و حتی جهان می تواند نسبت به کائنات به عنوان سیستم بسته ای فرض شود. تصویر 5-1 مثالی از یک حجم کنترل است که جریان انرژی از مرزهای آن(دیواره ی سیلندر) عبور می کند و موجب انبساط جرم و مقابله با نیروی(F) می شود. کاهش جریان حرارت موجب غلبه نیروی(F) و انقباض گاز می گردد. این سیستم نسبت به جریان جرم بسته است. در سیستم باز، انرژی و جرم بین محیط و سیستم عبور می کنند. سیستم ایزوله نیز سیستمی است که هیچ ارتباطی با محیط ندارد و جریان جرم یا انرژی از آن عبور نمی کند.

انرژی و انتروپی(Entropy) دو مفهوم بنیادی تحلیل های ترمودینامیکی هستند و از این نظر می توان، ترمودینامیک را علم انرژی و انتروپی نیز نامید. زیرا قواعد اصلی ترمودینامیکی بر پایه ی این دو مفهوم ارائه شده اند.

انرژی قابلیت و توانایی انجام کار است و فارغ از انواع، به طور کلی به دو شکل پتانسیل(Potential) و جنبشی(Kinetic) وجود داشته و ذخیره می شود.

چنانچه انرژی گرمایی(Thermal) را انرژی داخلی(Internal) مواد و ناشی از نیرو های بین مولکولی و حرکت مولکولها بدانیم، می توانیم انرژی پتانسیل را نیروی بین مولکولی مواد و انرژی جنبشی را سرعت حرکت مولکولها تعریف کنیم. انرژی پتانسیل وابسته به موقعیت نیز هست و بنا به مباحث دینامیک کلاسیک می توان مقدار ارتفاع و به تبع آن شتاب جاذبه را متناسب با انرژی پتانسیل دانست.

بنابراین مقدار انرژی پتانسیل از طریق رابطه ی زیر قابل محاسبه است:

( 1- 5 ) PE = mgz

PE : انرژی پتانسیل

m : جرم

g : شتاب جاذبه

z : ارتفاع از سطح افقی مبدا

همانگونه که اشاره شد انرژی جنبشی ناشی از سرعت مولکولهاست. بنابراین مقدار آن را می توان متناسب با سرعت، مطابق رابطه ی زیر تعیین کرد:

( 2- 5 ) KE = mV²/2

KE : انرژی جنبشی

V : سرعت

m : جرم

چگونگی چیدمان اتم ها و ترکیب مولکولی، انرژی شیمیایی(Chemical) و نیروی نگهدارنده پروتون ها و نوترون ها، انرژی اتمی یا هسته ای(Nuclwar) هستند.

سایر مفاهیم مورد استفاده در مباحث ترمودینامیک

گرما (Q) مکانیسمی برای انتقال انرژی از مرزهای یک سیستم بر اساس اختلاف دما است و جهت آن به سمت دمای کمتر است. یعنی انتقال گرما از جسمی با دمای بیشتر به جسمی با دمای کمتر صورت می گیرد.

کار نیز مکانیسمی از انتقال انرژی از مرزهای یک سیستم بر اساس اختلاف فشار یا نیروهای مشابه است و جهت آن همواره به سمت شرایط کم فشار است.

کار مکانیکی (W) نیز ناشی از جا به جایی یا جذب انرژی توسط مکانیسمی مانند توربین، کمپرسور هوای فشرده یا موتور احتراق داخلی است.

جریان کار نیز حمل یا انتقال انرژی به یک سیستم از محیط خارج سیستم است.

جریان کار به ازای جرم برابر است با فشار در حجم مخصوص یا حجم جا به جا شده به ازای واحد جرم :

( 3- 5 )                                                                                          PV=جریان کار به ازای واحد جرم

مشخصه های ترمودینامیکی یک سیستم شامل دما (T) فشار (P) ، حجم مخصوص (V) و چگالی (ρ) است.  سایر مشخصات ترمودینامیکی عبارتند از : انتروپی (s) و و انتالپی (h) و شکل انرژی از نظر پتانسیل و جنبشی و برخی از خواص ترکیبی، به عنوان مثال انتالپی متناسب است با انرژی داخلی به ازای وزن (u) به علاوه حاصل ضرب فشار در حجم مخصوص :

( 4 – 5 )                                                                                                     pv + u ≡ h

حالت سیستم نیز مرتبط با مشخصه های قابل اندازه گیری ترمودینامیکی است که در قالب دستگاه های مختصاتی بر اساس مولفه های مختلف مانند :

( فشار – دما ) ، ( دما – انتروپی ) ، ( فشار – انتالپی ) و یا ( فشار – حجم مخصوص ) تحلیل می شود.

فرایند حاصل تغییرات حالت است که منجر به تغییر برخی مشخصات سیستم می شود.

تعادل سیستم، میل سیستم برای متوازن شدن پس از یک فرایند یا تغییر حالت در یک سیستم است. در طول فرایند یا مرحله ی تغییر حالت، تعادلی وجود ندارد.

چرخه، حاصل چندین تغییر حالت متوالی یا فرایند است که سرانجام به حالت اولیه ختم می شود.

ماده خالص، ماده ای همگن با ترکیب شیمیایی تغییر ناپذیر است که می تواند در بیش از یک فاز وجود داشته باشد و در تمامی حالات ترکیب شیمیایی آن یکسان باقی بماند. آب مایع می تواند مخلوطی از مایع و بخار یا مخلوط مایع و یخ باشد و در عین حال ترکیب شیمیایی آن ثابت باقی بماند. در عین حال مخلوط هوای مایع و هوای گازی، ماده خالص محسوب نمی شود، زیرا ترکیب آن در دو حالت مایع و گاز متفاوت است.

اگر مایع در دما و فشار اشباع باشد ، مایع اشباع(Saturated Liquid) خوانده می شود.

اگر دمای مایع کمتر از دمای اشباع در فشار معین باشد، مایع مادون سرد(Subcooled) یا مایع متراکم شده(Compressed) نامیده می شود. مایع متراکم تحت فشار بیشتری از فشار اشباع در دمای معین است. چنانچه بخشی از ماده ی موجود مایع و بخشی دیگر بخار باشد، کیفیت براساس نسبت جرم بخار به جرم کل تعیین می شود. کیفیت ماده زمانی به آن اتلاق می شود که ماده دردما و فشار اشباع باشد.

اگر دمای بخار بیش از دمای اشباع آن باشد، آن را فوق داغ(Superheat) می نامیم و اگر دمای آن در دمای اشباع باشد، آن را بخار اشباع می نامیم و گاهی از اصطلاح بخار اشباع خشک برای کیفیت صد در صد آن استفاده می شود. فشار و دمای فوق داغ مستقل از یکدیگرند و می توان دما را مستقل از فشار و ثابت بودن آن افزایش داد. گازها را می توان بخار فوق داغ دانست.

انتروپی چیست

مفهوم انتروپی فارغ از علمی بودن ما را درگیر موضاعات فلسفی می کند، زیرا انتروپی بر بی نظمی و تحولات و گوناگونی حالت های ماده و انرژی دلالت دارد، که گاه در نظر گرفتن تمامی آن ها از دایره ی شناخت و پیش بینی خارج شده و اینجاست که فلسفه به عنوان مقدمه و ادامه دهنده علوم وارد بحث و گمانه زنی و نظریه پردازی می شود. شاید علم مقدمات فلسفه را تایید کند. در آن صورت شناخت علمی باز به مرزهایی خواهد رسید که مشاهدات و تجربیات مشخص و معینی در رابطه با آن وجود نداشته و یا حداقل تا مدت زمانی وجود ندارد. بنابراین بار دیگر گمانه زنی های فیلسوفانه و نظریه پردازی های مبتنی بر منطق و آرای فلسفی پا به میان می گذارند. این گونه است که می توانیم فلسفه را مقدمه و ادامه علوم بدانیم. انتروپی نیز از جمله مفاهیم پیچیده و نسبتا مبهمی است که میدان را برای نظریه پردازی های فلسفی باز می گذارد. اما از نظر ترمودینامیکی می توان انتروپی را درجه ای برای تعیین مقدار بی نظمی در یک سیستم بسته یا حجم کنترل دانست. به عبارت دیگر هر چه انتروپی بیشتر باشد ، درجه ی بی نظمی نیز بالاتر است. چنانچه نظم درونی مواد، مورد نظر باشد، می توانیم بگوییم که انتروپی گازها نسبت به مایعات و مایعات نسبت به جامدات بیشتر است، زیرا بی نظمی در آنها چنین نسبتی با هم دارند. چیزی که انتروپی را پیچیده و مرموزتر می کند، عدم امکان سنجش مستقیم آن به وسیله تجهیزات اندازه گیری است.  انتروپی را تنها می توان به صورت غیر مستقیم و از طریق به کار گیری روابط ریاضی تعیین کرد. به طور کلی اگر بخشی از مفهوم انتروپی را در جنبش و جوشش مولکولی مواد جستجو کنیم، می توان گفت که سیستم ها در دماهای کمتر تمایل بیشتری به نظم از خود نشان می دهند و به همین نسبت، انتروپی آنها کمتر است. نماد انتروپی s واحد آن KJ/MOL یا BTU/LB است. همانگونه که مشخص است دما و جرم هر یک نقش اصلی در مقدار انتروپی دارند.

انرژی نیز قابلیت انجام کار است و به صورت های مختلفی به کار گرفته می شود و در این میان گرما نوعی انرژی پایه محسوب می شود و میل به بی نظمی در آن از هر صورت دیگری بیشتر است. از این رو مصادیق انتروپی در مورد گرما بارزتر و گویاتر است و بر همین اساس یکی از ارکان مقداری انتروپی، دما است.

آنچه به صورت مقدماتی در مورد انرژی و انتروپی آمد، در قالب قواعد ترمودینامیکی شکلی منسجم تر و ریاضی وار به خود می گیرند. بنابراین در ادامه و به اختصار نگاهی به این قواعد خواهیم داشت.

مباحث ترمودینامیکی بر بستر چهار قانون که بیشتر مبتنی بر صحت تجربی هستند تحت عناوین قوانین صفرم، اول، دوم و سوم طرح می شود.

قوانین صفرم و اول بستری برای طرح مباحث انرژی است، اما قوانین دوم و سوم قطع نظر از طرح مباحث مربوط به انرژی به طرح انتروپی نیز می انجامد.

بر اساس قانون صفرم، چنانچه دوجسم با جسم سومی هم دما باشند با یکدیگر نیز هم دما هستند.

بر اساس قانون اول، انرژی داخلی یا درونی تفاضلی است بین انرژی داده شده به یک سیستم و کار گرفته شده از آن.

بر اساس قانون دوم، جهت جریان حرارت محدود و مشخص است. به این معنا که جریان حرارتی از جسم گرم به سرد است و عکس آن امکان پذیر نیست مگر آنکه کار انجام شود.

بر اساس قانون سوم، صفر مطلق یک دمای حد و رسیدن به آن به معنای سکون مطلق است. رسیدن و یا پایین تر رفتن از چنین حدی غیر ممکن است.

قانون اول ترمودینامیک

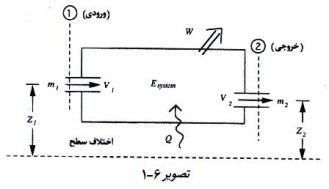
قانون اول ترمودینامیک اغلب قانون بقا یا پایستگی انرژی نامیده می شود. بر اساس این قانون، مقدار خالص انرژی اضافه شده به یک سیستم برابر است با افزایش انرژی ذخیره شده در سیستم. بنابراین انرژی از بین نمی رود، بلکه از شکلی به شکل دیگر در می آید. بر همین اساس می توان گفت که اختلاف انرژی ورودی و خروجی یک سیستم برابر است با افزایش انرژی سیستم. تصویر(6 – 1) جریان انرژی ورودی و خروجی را در یک سیستم ترمودینامیکی نمایش می دهد. در موارد عمومی برای جریان جرم ورودی و خروجی یک سیستم و تعادل انرژی در آن، روابط زیر مورد استفاده قرار می گیرد :

( 5 – 5 ) Ʃ^m_in(u + pv + v² / 2 + gz ) _in – Ʃ ^m_out ( u ++ v² / 2 + gz ) _out + Ǫ – w

= [ m_ƒ ( u + v² / 2 + gz )_ƒ – m_i ( u + v² / 2 + gz )_i ]_system

در جریان پایدار یا حالت پایدار که معادلات آن برای تحلیل تجهیزاتی همچون کمپرسورها، دیگ ها و کندانسورها مورد استفاده قرار می گیرد، شرط این است که حالت جرم در هر نقطه از حجم کنترل نسبت به زمان تغییر نکند. این نوع سیستم ها باز هستند و جریان جرم در نقطه یا نقاطی به آن وارد و از نقطه یا نقاطی از آن خارج می شود. در نتیجه خواهیم داشت :

( 6 – 5 )

در رابطه ی دوم(ṁ) دبی جرمی جریان است. چنانچه در رابطه اول به جای(u+pv) معادل آن یعنی(h) جای گیرد و طرف دوم معادله نیز ساده شود، رابطه ی زیر به دست خواهد آمد :

( 7 – 5 ) Q – W = [ m ( u_f – u_i ) ]_system

و یا می توان گفت که تغییرات انرژی یک سیستم برابر است با مجموع گرمای داده شده و کار انجام شده :

( 8 – 5 ) ΔU = Q + W

قانون دوم ترمودینامیک

بر اساس قانون دوم ترمودینامیک جهت جریان یک فرایند تنها در یک جهت است و در خلاف جهت، امکان وقوع و پیش روی جریان وجود ندارد. به عنوان مثال در حالت طبیعی همواره انتقال حرارت از جسم گرم به جسم سرد صورت می گیرد و امکان انتقال گرما در جهت عکس، یعنی از جسم سرد به جسم گرم وجود ندارد. بنابراین در فرایندها باحالت های خود به خودی روبه رو خواهیم بود که از آنها نمی توان گریخت، و البته وجود حالات خود به خودی به معنای عدم وجود احتمالات در همان جهت و راستا نیست. اینجاست که انتروپی به عنوان بیان کننده ی فرایندهای خود به خودی موضوعیت پیدا می کند. انبساط گازها و یا سرد شدن جسم تا رسیدن به دمای محیط از جمله فرایندهای یک سویه یا بازگشت ناپذیری هستند که در نتیجه آنها انتروپی افزایش می یابد. این خود نوعی به تعادل رسیدن است، بنابراین نمی توان بی نظمی مصطلح در مورد انتروپی را منجر به عدم تعادل دانست. بی نظمی منتسب به انتروپی در واقع نوعی نگرش قراردادی است که در اصل با تعادل در تباین قرار می گیرد. با نگاهی خرده انگارانه می توانیم بگوییم که با روشن کردن یک کبریت به انتروپی جهان افزوده ایم؛ اما در این نگرش مقدار اثر گذاری مغفول واقع می شود. درست است که بگوییم اگر گرما از منبع گرم به منبع سردی منتقل شود انرژی جریان یافته و کاری انجام می شود و این جریان یک سویه با کاهش انرژی و افزایش انتروپی همراه است. به عبارت دیگر می توان گفت که انتقال انرژی از منبعی گرم تر به منبعی گرم، توام با انتروپی کمتری نسبت به انتقال انرژی از منبعی گرم به منبعی سرد است. قانون دوم ترمودینامیک از دو دیدگاه بیان می شود. یک دیدگاه که به نام کلوین – پلانک معروف است، بیان می دارد که در یک فرایند تبدیل انرژی گرمایی به کار هیچ گاه تبدیل کامل ممکن نیست. در واقع بازده عملکرد حاصل از کار یک موتور یا ماشین گرمایی که انرژی حرارتی را به کار مکانیکی تبدیل می کند، صد در صد نیست و بخشی از انرژی به صور دیگر از سیستم خارج می شود. این بیان نه تنها ناقض قانون اول ترمودینامیک نیست، بلکه در راستای همان تجربیات قرار می گیرد.

دیدگاه دیگر که بیان کلازیوس خوانده می شود، بیان می کند که انتقال گرما از یک جسم سرد به یک جسم گرم تر بدون انجام کار ممکن نیست. هر دو دیدگاه به گونه ای منفی و در جهت نفی امکان مشخصی هستند. بیان کلوین تبدیل صد در صد انرژی به کار را نفی می کند و بیان کلازیوس ساخت سیستم سرمایشی ایده ال را منکر می شود. دیدگاه کلازیوس بر حتمی بودن استفاده از کار مکانیکی برای عمل سرمایش تاکید دارد و از این نظر می تواند برای موضوع این کتاب که بحث در خصوص چیلرهای جذبی را محور کار قرار داده است، مهم و حائز اهمیت ویژه باشد. در هر حال این دو دیدگاه هم ارز یکدیگر هستند و با نقض یکی از آنها، دیگری نیز نقض می شود. از این نظر دیدگاه کلوین – پلانک نیز در ارتباط با موضوع کتاب حاضر نقش مهمی پیدا میکند. در واقع تمامی مباحثی که پس از این در مورد ضریب کارایی طرح خواهد شد، برگرفته از چنین دیدگاهی است. فرایندهای بازگشت ناپذیر در یک چرخه ی سرمایش که به طور قطع نیازمند اعمال کار مکانیکی است شامل افت فشارها در خطوط و مبدل ها و اصطکاک مکانیکی می شود. با کاهش فرایندهای بازگشت ناپذیر، بازده چرخه ی فرایند سرمایش افزایش پیدا می کند. در یک سیستم باز برای بیان قانون دوم ترمودینامیک بر اساس مفهوم انتروپی می توان چنین رابطه ای را نوشت :

( 9 – 5 )                                                                          dS_system = δǪ / T +δm_is_i – δm_es_e + dI

dS_system : تغییرات انرژی کل در واحد زمان در خلا فرایند

δmisi : افزایش انتروپی ناشی از جرم ورودی

δm_es_e : کاهش انتروپی ناشی از جرم خروجی

δǪ / T : تغییرات انتروپی ناشی از فرایند برگشت پذیر تبادل حرارت بین سیستم و محیط

dI :  انتروپی ایجاد شده ناشی از فرایند بازگشت ناپذیر که همواره مقداری مثبت است .

معادله فوق را می توان بر اساس تغییرات انتروپی به صورت زیر نوشت :

( 10 – 5 )                                                                      δǫ = T [( δmese – δmisi) + δSsys – dI ]

مقدار تغییر انتروپی در فرایند های بازگشت پذیر و بازگشت ناپذیر یکسان است، بنابراین تعیین این تغییرات در یک مسیر به منزله تعیین مقدار در مسیر دیگر نیز هست. رابطه عمومی قانون دوم را می توان بر اساس انتگرال گیری از نرخ انتقال حرارت و دما و بر اساس تغییرات انتالپی به صورت زیر نوشت :

( 11 – 5 ) ( S_ƒ – S_i ) _system = ∫_rev δǪ / T + Ʃ^{( ms )}_in – Ʃ^{( ms)}_out + I

در نظر نگرفتن زمان و یکنواختی چرخه های کاربردی منجر به عدم تغییرات انتروپی می شود. بنابراین در این صورت انتروپی صفر شده و رابطه ی بالا را می توان برای چنین چرخه هایی و برای تعیین نرخ بازگشت ناپذیری به صورت زیر نوشت :

( 12 – 5 ) I = Ʃ^{( ms )}_out – Ʃ^{( ms )}_in – ∫ Ǫ / T_surr

اگر دمای محیط برابر با دمای سیستم باشد معادله بالا برابر صفر خواهد شد. با ترکیب معادله ی بالا با معادله ی ( 6 – 5 ) معادله ی ( 13 – 5 ) به دست می آید :

( 13 – 5 )                                                                    I = m [ ( S_out – S_in ) – h_out – h_in / T_surr ]

در چرخه های واقعی که بنا به دلایل مختلف نیازمند صرف کار بیشتری می شوند، مقدار کار مورد نیاز چرخه ی واقعی برابر است با دمای مطلق محیط به علاوه ی کار مورد نیاز ناشی از فرایندهای بازگشت ناپذیر. بنابراین کار واقعی را می توان از طریق رابطه ی زیر محاسبه کرد.

( 14 – 5 ) W_actual = W_reversible + T₀Ʃ^I

در چرخه های سرمایشی انتقال انرژی از یک ناحیه با دمای کم به یک ناحیه با دمای زیاد صورت می گیرد. به طور معمول ناحیه یا سیال دمای زیاد می تواند یک سطح حرارتی یا هوای محیط باشد.

ضریب کارایی یک سیستم سرمایشی نسبتی است بین سرمایش مفید(مقدار گرمای خارج شده از سیستم) به مقدار انرژی خالص ورودی به سیستم از منبع خارجی .

( 15 – 5 )                                            سرمایش مفید / مقدار انرژی خالص ورودی از منبع خارجی = COP

در سیستم های مکانیکی تراکم بخار، انرژی اولیه یا ورودی به طور معمول شکلی از کار ناشی از عملکرد تجهیزات مکانیکی یا الکتریکی مانند کمپرسورها است. بنابراین می توان نوشت :

( 16 – 5 ) COP = Ǫ_i / W_net

در سیستم های سرمایش جذبی، انرژی حرارتی به طور مستقیم از یک مولد گرمایشی تامین می شود و در کنار آن کار مکانیکی ناشی از کارکرد پمپ ها و فن ها(مانند فن برج) نیز دخیل هستند. بنایراین در این مورد می توان نوشت :

( 17 – 5 )    COP = Ǫ_i / Ǫ_gen + W_net

به طور معمول در سیستم های جذبی، انرژی ورودی به شکل کار در مقایسه با انرژی گرمایی ورودی بسیار اندک و قابل اغماض است. مقدار انحراف ضریب کارایی واقعی از ضریب کارایی بازگشت پذیر ایده آل، بازده سیستم را تعیین می کند :

( 18 – 5 )                                                  COP / ( COP )_rev =η_R

چرخه ی کارنو

چرخه ی کارنو، چرخه ای بازگشت پذیر است که بین دو منبع دمای ثابت عمل میکند. این چرخه ی تراکمی در یک وضعیت همچون یک نیروگاه بخار عمل نموده و در جهت عکس تبدیل به یک سیستم سرمایش تراکمی می شود. چرخه ی کارنو که از دو فرایند هم دما و دو فرایند آدیاباتیک تشکیل شده است.

با انجام برخی عملیات پیشگیرانه می توان از بروز عیب در چیلرهای جذبی جلوگیری کرد که پیش از این برخی از این موارد یادآوری شد. در اینجا به طور فهرست وار این موارد را از نظر می گذرانیم.

نمونه گیری و آزمایش

محلول برای سیستم هایی که در تمام سال کار می کنند هر چهار ماه یک بار و برای سیستم هایی که در طول سال فقط برای تابستان مورد استفاده قرار می گیرند سالی یک بار انجام گیرد.

ثبت اطلاعات عملکردی 

باید کلیه شرایط عملکردی چیلر، مانند دما و فشار قسمت های مختلف به صورت روزانه توسط تیم راهبری ثبت شود تا به هنگام بروز عیب بتوان شرایط پیش آمده را تحلیل کرد.

نشت یابی سیستم

در صورت جمع شدن بیش از اندازه ی گازهای غیر قابل تقطیر، سیستم باید به طور کلی مورد آزمایش نشتی قرار گیرد.

کنترل اتصالات و مدارهای الکتریکی

حداقل سالی یک بار کلیه سیستم های الکتریکی و مدار فرمان باید مورد بازبینی قرار گیرد.

تعویض شیشه رویت و واشر آن

چنانچه شیشه رویت شفافیت خود را از دست داده باشد و سطح محلول به خوبی دیده نشود، باید شیشه رویت را برای پرهیز از هرگونه اشتباهی تعویض کرد. همچنین ممکن است واشر دور شیشه ی رویت موجب ایجاد نشتی شود، که در این صورت این واشر هم باید تعویض شود.

کنترل مقدار الکل اکتیل

در صورت اختلال در ظرفیت برودتی چیلر، باید میزان الکل اکتیل مورد بازبینی قرار گیرد.

بازبینی کنترل کننده ها

بهتر است سالی یک بار، کنترل کننده هایی مانند کلید قطع کننده دمای کم مبرد، فلوسوئیچ ها و کلید قطع کننده دمای بالا مورد بازبینی قرار گیرند.

بازبینی حسگرها

بهتر است سالی یک بار، دقت حسگرهای دما و فشار مورد بازبینی قرار گیرند.

بازبینی پمپ ها

وجود ذرات رسوب و فلزات می توانند موجب آسیب دیدگی یاتاقان های پمپ شوند. بنابراین بهتر است هر چهار سال یک بار پمپ ها مورد بازرسی اساسی قرار گیرند. هر سال یک بار نیز باید کنتاکتورها و رله های اضافه بار پمپ ها را مورد بازرسی قرار داد و اتصالات الکتریکی آن را کنترل کرد. جریان وگرمای پوسته پمپ نیز از جمله موارد مهم است که باید به آنها توجه کرد.

بازرسی پمپ خلا و سیستم تخلیه گازهای غیر قابل تقطیر

باید هر شش ماه یک بار و در صورت نیاز تسمه پمپ را تعویض کرد و به طورماهیانه مقدار جریان الکتریکی آن را کنترل کرد. همچنین توجه به روغن پمپ هم از کمی و هم از جهت کیفی بسیارمهم است. هر شش ماه می باید دقت مانومتر سیستم خلا مورد بازبینی قرار گیرد.

بازبینی کوئل های ابزوربر، کندانسور و اواپراتور

هر سال یک بار می باید کلیه لوله ها و کوئل های چیلر برای تعیین میزان رسوب گذاری مورد بازبینی قرار گیرد.

بازدید از لوله کشی های خارجی چیلر

به طورمرتب و روزانه، کلیه لوله کشی های متصل به چیلر، اعم از بخار، چگالیده، آب برج خنک کننده و آب سرد باید مورد بازبینی قرار گیرد.

تفاوت اصلی بین سیستم های جذبی و تراکمی در اینست که درسیستم جذبی به جای استفاده از انرژی مکانیکی برای ایجاد تغییرات لازم در ماده سرمازا به منظورتکمیل سیکل تبرید، از انرژی حرارتی استفاده می شود. در سیستم جذبی ممکن است از گاز، نفت و یا گرمای الکتریکی برای ایجاد حرارت استفاده می شود. این سیستم دارای کمترین تعداد قطعات متحرک است و در سیستمهای کوچکتر قطعات متحرک فقط به سوپاپها و کنترل های معمول منحصر می شود. ولی در بعضی از دستگاههای بزگتر علاوه بر سوپاپها و کنترلها از پمپ های جریان دهنده ی ماده سرمازا و پنکه نیز استفاده می شود. سیستم های جذبی موقع کار آرام و بی صدا هستند و در تاسیسات تجارتی و خانگی مورد استفاده واقع میشود. از سیستمهای تبرید جذبی بطور گسترده ای درکامیونهای پخش نوشابه و بستنی و غیره، اردوگاه ها، کاروانها و قایق ها استفاده به عمل آمده و از آنجا که میتوان آنها را با یک سیلندر کوچک گاز بکار انداخت، به موارد استفاده از آنها به عنوان یک دستگاه قابل حمل افزوده است.

1-1 سیستم جذبی             

شکل 1-1 اجزاء اولیه یک سیستم جذبی را نشان میدهد. سیستم جذبی نشان داده شده در این شکل، بمنظور قیاس با سیستمهای سرد کننده مکانیکی از نوع مجهز به جاذب جامد انتخاب شده است. کلاف کندانسور، مخزن تجمع مایع و اواپراتور(کلاف سرد کننده) کاملا شبیه قطعات مشابه سیستمهای تراکمی هستند ولی کمپرسور جای خود را به گرمکن یا مولد داده است. به منظور ساده کردن تصویر برای مقایسه، کنترلهای مختلف از آن حذف گردیده است. شکل 2-1 یک نوع سیستم جذبی ابتدایی از نوع مجهز به مایع جاذب را که در آن از کندانسور آبی استفاده می شود نشان می دهد.

2-1 انواع سیسیتمهای جذبی 

ترکیبات متعددی از مواد وجود دارند که دارای خواص غیر عادی هستند، مثلا یکی از مواد ممکن است بدون وقوع فعل و انفعالات شیمیایی ماده دیگر را جذب کند، و یا ممکن است ماده ای ماده دیگر را در حالت سردی جذب کرده و پس از گرم شدن رها سازد. اگر این ماده جامد باشد عمل را گاهی جذب و اگر ماده سیال باشد این عمل را همیشه جذب می نامند. دو نوع یخچال جذبی وجود دارد که در یکی از انها از ماده جاذب جامد و در دیگری از ماده جاذب سیال استفاده می شود. این دو نوع یخچال جذبی تحت عنوان ” اصل فاراده ” که ماده جاذب آن جامد است و یخچال الکترولوکس که ماده جاذب آن سیال است طبقه بندی میشوند. نوع دیگری از طبقه بندی سیستم جذبی بر مبنای عوامل زیر است :

1- سیستم  جذبی متناوب                                                            2- سیستم جذبی پیوسته

سیسیتم های جذبی ، کاربردهای متعددی به قرار زیر داشته اند :

1-  خانگی                                      2- صنعتی                                                      3- تهویه

سیستم های جذبی بر حسب نوع و منبع حرارتی بکار رفته نیز بصورت زیر طبقه بندی میشوند :

1- نفتی                                      2- گازی ( طبیعی یا مصنوعی )                               3- الکتریکی

برخی از سیستمهای جذبی که در کاروانهای خانوادگی بکار میروند احتمالا بوسیله نیروی برق ویا سوخت کم فشار گرم میشوند ، این سیستمها در بخش3-1تشریح شده اند.

3-1 اصول سیستم جذبی  جامد  

میشل فاراده در سال 1824 یک سلسله آزمایش برای تبدیل بعضی گازهای پایدار به مایع، که دانشمندان معتقد بودند این مواد فقط به شکل گاز(بخار) وجود دارند انجام داد. در بین این گازها، آمونیاک(717- (Rکه همیشه به نام یک گاز پایدار شناخته شده بود نیز وجود داشت. فاراده میدانست که کلرور نقره که پودری سفید است دارای خاصیت غیر عادی جذب مقادیر زیادی گاز آمونیاک است، بنابراین پودر کلرور نقره را در مجاورت گاز خشک آمونیاک قرار داد و هنگامی که پودر کلرور نقره تمام امونیاک ممکن را جذب کرد مخلوط آمونیاک و نقره را در یک لوله آزمایش که به صورت 8 تا شده بود مسدود کرد و سپس یک انتهای لوله را که حاوی مخلوط بود حرارت و انتهای دیگر آنرا بوسیله آب مطابق شکل 10-3 از فصل سوم سرد کرد. حرارت، گاز آمونیاک را رها نموده و بزودی قطرات بیرنگ مایع شروع به ظهور در انتهای سرد شده لوله نمودند و بنابراین آمونیاک مایع تولید گردید. فاراده به عمل حرارت دادن ادامه داد تا مقدار کافی آمونیاک که موردنظرش بود بدست آمد، سپس شعله را خاموش کرد و به مطالعه ماده جدیدالکشف خود پرداخت. چند لحظه پس از خاموشی شعله، فاراده متوجه واقعه ای غیر عادی شد، آمونیاک مایع در لوله بجای آرام ماندن شروع به غلیان و جوشیدن شدید نمود وسریعا به حالت گازی برگشت و گاز حاصل مجددا بوسیله پودر کلرور نقره درانتهای دیگر لوله جذب گردید. با لمس کردن انتهای حاوی مایع جوشان، فاراده با کمال تعجب دریافت که آن قسمت به شدت سرد شده است. و نتیجه گرفت که آمونیاک، هنگام تبدیل شدن از مایع به گاز حرارت جذب نموده و این گرما را از نزدیکترین جسم به خود که همان لوله آزمایش بوده گرفته است.

4-1 اصول سیستم تبریدجذبی پیوسته

سیستم جذبی مایع دارای بعضی خواص خوب است. آب تحت درجه حرارت و فشار عادی مقدار زیادی گاز آمونیاک را جذب میکند (717-   (Rوآمونیاک محلول در آب بسهولت بوسیله حرارت دادن آب احیا میشود، همچنین گرمای نهان تبخیر آمونیاک مایع آنقدر زیاد است که هنگام تبدیل شدن به بخار مقدار زیادی گرما به خود جذب میکند . SERVEL نوعی یخچال خانگی است که بر مبنای جذب سیکل یپوسته طرح شده و فاقد هر گونه قطعات متحرک یا سوپاپ است(غیر از قطعاتی که برای کنترل شعله کوره یا مشعل آن بکار میرود). ماده سرمازای یخچال آمونیاک و حلال آن آب است. برای ایجاد فشار جزئی آمونیاک(طبق قانون دالتون مبحث 53-1) و ایجاد امکان تبخیر آن در فشار کم از گاز هیدروژن استفاده میشود. در شکل 3-1 ، A  نماینده آمونیاک و H نماینده هیدروژن است. زمانی که کوره در(1) روشن شده و گرمای آن به قسمت میانی مولد منتقل شود(1) بخارداغ آمونیاک از محلول متصاعد شده و در قسمت(1b) از میان لوله غلیان(10) به سمت بالا حرکت میکند و در ضمن حرکت در این لوله محلول را با خود به سطح بالایی جدا کننده(11) می برد. بیشتر محلول مایع در ته(11) باقی مانده و از طریق مبدل گرما(9) به طرف قسمت جاذب گرما(4) حرکت میکند. بخار داغ آمونیاک بعلت سبکی به بالای لوله(11) رفته و سپس از طریق لوله میانی به قسمت تجزیه کننده(6) سرازیر میگردد و در اینجا هر گونه محتوی بخا رآب از آن گرفته شده بخار داغ و خالص آمونیاک به طرف بالا و یکسو کننده(7) می رود. یکسو کننده(7) شامل تعدادی پره و صفحات کوچک است که لوله را احاطه کرده اند، اگر بخار داغ آمونیاک در این مرحله هنوز هم دارای مقداری بخار آب باشد برای اطمینان از خلوص کامل آن باید بخار آب از آن گرفته شود. در این نقطه گرما کار خود را کامل کرده و برای طی باقیمانده مدار گردش، نیروی طبیعی جاذبه است که ادامه جریان را سبب میشود.

بخار خالص و داغ آمونیاک به کندانسور(2) می رود و هوای نسبتا خنک محیط که از میان پره ها عبور مینماید گرمای بخار آمونیاک را گرفته و مقداری از آن را تقطیر و در(2a) به مایع تبدیل میکند. این آمونیاک حالا به صورت کاملا خالص است و تحت نیروی جاذبه به اواپراتور(3a) جریان می یابد. و مقداری زخارآمونیاک که تقطیر نشده به(2b) رفته و در آنجا تقطیرمیشود و در لوله بالایی یا تله آمونیاک جمع میشود. لوله های خمیده ای( U-tube) که از کندانسور منشعب می شوند، به عنوان محل تجمع آمونیاک مایع هستند که در آنها آمونیاک تا ارتفاع معینی جمع شده و سپس به اواپراتور(3a) سرازیر میشود(بخاطر اصل ظروف مرتبط). مایع آمونیاک پس از سرازیر شدن به کلافهای تبخیر(3aو3b) به صورت برکه های کم عمقی در روی تعدادی صفحات افقی قرار میگیرد. گاز هیدروژن که به مقدار زیاد وارد کلافها میشود، سبب میگردد که آمونیاک مایع در درجه حرارت کمتری تبخیر شود(طبق اصل دالتون) آمونیاک، گرمای تبخیر خود را از کابینت یخچال گرفته و سبب انجماد آب در قالبهای جا یخی میشود. هر چه مقدار هیدروژن بیشتر ومقدار آمونیاک کمتر باشد درجه حرارت کمتری تولید میشود(سرمای بیشتر) بخار حاصله از تبخیر آمونیاک مایع با گاز هیدروژن مخلوط میشود و چون وزن مخلوط از هیدروژن سنگین تر است از قسمت میانی مبدل گرمای گاز(8) به قسمت جاذب(4) میرود. این جریان در اواپراتور بطور پیوسته ادامه می یابد و مخلوط هیدروژن و بخار آمونیاک که از قسمت میانی مبدل گرمای گاز میگذرد، گاز هیدروژن خالص را که در لوله خارجی صعود می کند سرد می کند. در این هنگام محلول ضعیفی از آمونیاک و آب تحت نیروی جاذبه از مولد(1) و از طریق مبدل گرمای مایع(9) به طرف پایین و به بالای آب جاذب یا حلال سرازیر می شود. و در اینجا با مخلوط گاز هیدروژن و بخا ر آمونیاک که از اواپراتور و از طریق مبدل گرمای گاز می آید برخورد می کند. در اینجا محلول ضعیف و نسبتا سرد، بخار آمونیاک را جذب میکند، ولی چون هیدروژن درآب محلول نیست بصورت آزاد باقی مانده و بعلت سبکی به سطح قسمت جاذب آمده و از طریق مبدل گرمای گاز(8) و به اواپراتور باز میگردد. قسمت جاذب گرما(4) دارای تعدادی پره است و بوسیله هوا خنک میشود. و سرد شدن محلول ضعیف به جذب آمونیاک از مخلوط بخار آمونیاک و گاز هیدروژن کمک می کند. همچنین هنگامی که محلول ضعیف آب و بخار آمونیاک گاز آمونیاک را جذب میکند مقدار قابل توجهی گرما آزاد میشود که پره های خنک کننده بمنظور ادامه عمل سردکنندگی این گرما را گرفته و به هوای محیط پس میدهند. مبدل گرمای مایع، محلول قوی یا محلول آمونیاک مایع و آب را به تجزیه کننده(6) و از آنجا به مولد و جایی که سیکل سردکنندگی مجددا شروع میشود هدایت میکند. این دستگاه، مجموعه ای جوش داده شده است و هیچ قطعه متحرکی که در معرض فرسودگی و  خرابی باشد و از تنظیم خارج شود ندارد. فشار کل در طی سیکل و تحت درجه حرارت محیط 150 درجه فارانهایت تقریبا درحدود 400 پوند متعارفی است که الزاما استفاده از ساختمانی محکم و با دوام را ضروری مینماید. برای ایجاد صفر درجه سرما، آمونیاک موجود در اواپراتور باید در 7/15 پوند بر اینچ مربع بجوش آید، یعنی هیدروژن باید باقی مانده فشار، یعنی3/348 پوند بر اینچ مربع را تامین می کند تا فشار کل سیستم در 400 پوند متعارفی حفظ شود. این یخچال در میان یخچالهای خانگی منحصر بفرد است و شرح بیشتر آن در مبحث 8-1 آمده است.

5-1  اصول سیستم تبرید جذبی متناوب

مناسبترین سیکل یخچال برای مناطقی که به برق و گاز دسترسی ندارند، سیکل سوپر فکس(1) و تروکلد(2) است. سیکل سوپر فکس اساسا همان اصل فاراده است منتها چیزهایی اضافی نیز دارد که لازم به توضیح است. همانطور که در شکل 4-1 دیده می شود، آمونیاک و آب در مخزنی مسدود یا مولد(A) مخلوط می شوند که در زیر آن اجاق نفت سوز M قرار گرفته است. وقتی اجاق روشن میشود، گرمای حاصله آمونیاک را بصورت بخار درآورده از مخلوط جدا میکند. این بخار آمونیک از طریق یک لوله(D) به کلاف E  غوطه ور در آب مخزن B در بالای یخچال وارد میشود. سردی آب باعث تبدیل بخار آمونیاک به قطرات آمونیاک مایع تحت فشار تولید زیاد میشود. آمونیاک مایع ازطریق لوله ای بدرون مخزن تجمع مایع(C) میریزد و از اینجا به اواپراتورK که با محلول آب  نمک(H) احاطه شده میرود. برای جلوگیری از عمل کردن مخزن تجمع مایع به عنوان اواپراتور و سرد کردن بیش از حد کابینت، اطراف آن بالای عایق F پوشیده شده است. این عمل برای مدت نسبتا کوتاهی ادامه می یابد و پس از تمام شدن نفت و خاموش شدن اجاق، متوقف میشود. با خنک شدن قسمت جاذب گرما تا حد گرمای محیط، امونیاک در اواپراتور تحت درجه حرارت کم شروع به تبخیر میکند، زیرا با سرد شدن مولد، میل به جذب مجدد بخار آمونیاک میکند و در نتیجه فشار را کاهش داده، به آمونیاک امکان می دهد، تحت درجه حرارت کم در اواپراتور به جوش آید و این تبخیر است که باعث تولید سرمای لازم برای خنک کردن کابینت مواد غذایی می شود.

پس از خاموش شدن اجاق، درجه حرارت آب موجود در مولد(A) بسرعت به حرارت محیط میرسد و چون آب سرد میل ترکیبی فراوانی با آمونیاک دارد، آمونیاک بخار شده در اواپراتور از طریق لوله G به مولد بازگشته و مجددا با آب مخلوط میگردد و مطابق آنچه در شکل 5-17 دیده می شود

فشار نسبتا کمی را در اواپراتور حفظ میکند.

به عبارت دیگر، گرمای اجاق، آمونیاک را در مدت کوتاهی از مولد A به کلاف تبخیر(K) منتقل می کند، آمونیاک در اواپراتور تبخیر شده و به آهستگی و طی 24 ساعت تا 36 ساعت به مولد باز می گردد. و این تبخیر آمونیاک در اواپراتور است که عامل ایجاد سردی است. برای ازدیاد راندمان در مناطق گرم و یا برای سرد کردن مقادیر خیلی زیاد مواد غذایی میتوان در بالای مخزن کندانسور فرو رفتگی ایجاد نمود و آنرا پر از آب کرد، این آب بسرعت تبخیر شده و به سرد شدن مخزن کمک میکند. این نوع دستگاه سرد کننده در مبحث 7-1 به همراه سیستم تروکلد که اساسا شبیه آن است به تفصیل تشریح شده است. برای پیشگیری از انفجار سیستم دراثر پیدائی درجه حرارتهای زیاد(175 تا 200 درجه فارنهایت) در قسمتهای مختلف سیستم درپوشهای ذوب شونده ای تعبیه شده است و این پیش بینی بویژه برای مواقع بروز آتش سوزی که از انفجار کلی دستگاه جلوگیری میکند بسیار سودمند است.